Trigonometry, a branch of mathematics, delves into the relationships between the angles and sides of triangles. Though it may initially appear daunting, mastering trigonometry is crucial for students and professionals in various fields, including engineering, physics, architecture, and even computer science. This comprehensive guide will explore the essential concepts of trigonometry, provide practical examples, and explain how it applies to real-world scenarios.
Table of Contents
ToggleThe Trigonometric Ratios
At the heart of trigonometry lies the study of right-angled triangles. In such a triangle, one angle is always 90 degrees, and the relationships between the angles and sides are described using trigonometric ratios. The three primary trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These ratios are defined as follows:
- Sine (sin): The ratio of the length of the opposite side to the hypotenuse.
- Cosine (cos): The ratio of the length of the adjacent side to the hypotenuse.
- Tangent (tan): The ratio of the length of the opposite side to the adjacent side.
Given a right-angled triangle with angle θ, the sides are often labeled as follows:
- The side opposite angle θ is the “opposite” side.
- The side adjacent to angle θ (but not the hypotenuse) is the “adjacent” side.
- The hypotenuse is the longest side, opposite the right angle.
Using these definitions, the trigonometric ratios are expressed as:
sin(θ) = opposite/hypotenuse
cos(θ) = adjacent/hypotenuse
tan(θ) = opposite/adjacent
The Inverse Trigonometric Functions
In addition to the basic trigonometric functions, there are inverse functions—arcsine (sin⁻¹), arccosine (cos⁻¹), and arctangent (tan⁻¹). These functions are used to determine the angles when the ratios are known. For instance, if you know the sine of an angle, you can use the arcsine function to find the angle itself.
θ = sin⁻¹(opposite/hypotenuse)
θ = cos⁻¹(adjacent/hypotenuse)
θ = tan⁻¹(opposite/adjacent)
Extending to the Unit Circle
The unit circle is a fundamental concept in trigonometry that extends the definitions of the trigonometric functions beyond right-angled triangles. A unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. Any point on this circle can be represented by coordinates (x, y), where:
- x is the cosine of the angle formed with the positive x-axis.
- y is the sine of that angle.
In the context of the unit circle, the angle θ is measured in radians, where:
- 0 radians correspond to 0°.
- π/2 radians correspond to 90°.
- π radians correspond to 180°.
- 3π/2 radians correspond to 270°.
- 2π radians correspond to 360°.
The unit circle allows trigonometric functions to be applied to any angle, including those greater than 90 degrees or negative angles, by considering their corresponding points on the circle.
The Pythagorean Identity and Other Key Identities
Trigonometry is also built upon several fundamental identities that are derived from the relationships between the trigonometric functions. The most important of these is the Pythagorean Identity, which is based on the Pythagorean Theorem.
For any angle θ:
sin²(θ) + cos²(θ) = 1
This identity is invaluable for simplifying trigonometric expressions and solving equations. Other important identities include the angle sum and difference identities:
Sum Identities:
sin(α + β) = sin(α)cos(β) + cos(α)sin(β)
cos(α + β) = cos(α)cos(β) – sin(α)sin(β)
Difference Identities:
sin(α – β) = sin(α)cos(β) – cos(α)sin(β)
cos(α – β) = cos(α)cos(β) + sin(α)sin(β)
These identities are crucial for solving more complex trigonometric problems, particularly in calculus and advanced mathematics.
Applications of Trigonometry in Real Life
Trigonometry is not just an abstract mathematical discipline; it has numerous real-world applications. Here are a few key examples:
1. Engineering and Architecture
Engineers and architects frequently use trigonometry to calculate forces, angles, and distances. For example, in civil engineering, trigonometry is used to determine the correct angles for slopes and inclines in the construction of roads and bridges. In architecture, it helps in designing structures with the correct angles and dimensions.
2. Physics
Trigonometry plays a crucial role in physics, particularly in the study of waves, oscillations, and optics. For example, the sine and cosine functions describe the behavior of waves, such as sound waves, light waves, and radio waves.
3. Astronomy
Astronomers use trigonometry to calculate the distances between celestial bodies. By observing the angle formed by the line of sight from two different points on Earth to a star, astronomers can determine the star’s distance using trigonometric principles.
4. Navigation
Trigonometry is essential in navigation, both maritime and aerial. It helps in determining a ship or aircraft’s position by using the angles between fixed points on the Earth’s surface or in the sky.
5. Computer Graphics
In computer graphics, trigonometry is used to model and render objects, simulate lighting, and calculate object rotations. It’s fundamental in creating realistic animations and video games.
Advanced Trigonometric Concepts
As you delve deeper into trigonometry, you encounter more advanced topics, such as:
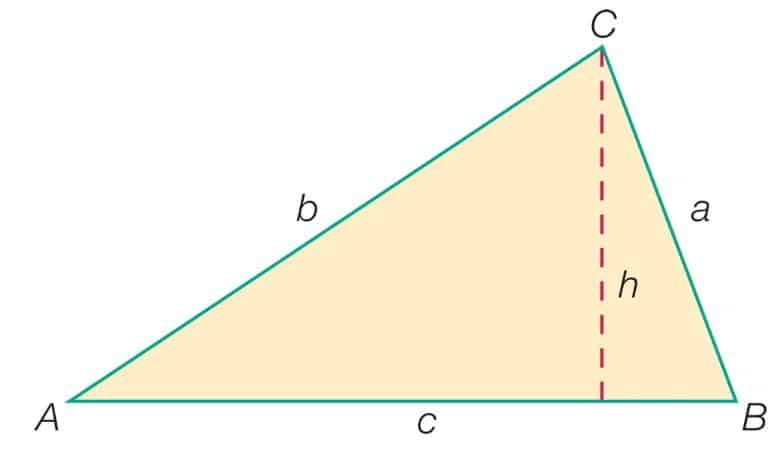
1. Law of Sines and Law of Cosines
These laws are used to solve any triangle, not just right-angled ones. The Law of Sines relates the lengths of the sides of a triangle to the sines of its angles:
a/sin A = b/sin B = c/sin C
The Law of Cosines generalizes the Pythagorean Theorem for any triangle:
c² = a² + b² – 2ab cos C
2. Trigonometric Equations
Solving trigonometric equations often requires manipulating identities, using the unit circle, and applying algebraic techniques. These equations are essential in calculus and other higher-level mathematics.
3. Polar Coordinates
Trigonometry is closely related to polar coordinates, a system where each point on a plane is determined by an angle and a distance from a fixed point. This system is particularly useful in physics and engineering for solving problems with symmetry.
4. Fourier Series and Transforms
In more advanced mathematics and engineering, trigonometry is fundamental to Fourier analysis, which decomposes functions into
their sinusoidal components. Fourier series and transforms are used in signal processing, quantum mechanics, and many other fields.
Conclusion
Trigonometry is a fascinating and essential area of mathematics with numerous practical applications. Whether you’re a student looking to understand the basics or a professional needing to apply trigonometric principles, mastering the essentials of trigonometry is crucial. With the concepts and techniques outlined in this guide, you’ll be well-equipped to tackle trigonometric problems and apply them in real-world scenarios.